A partir de la version 0.9.92, la tortue peut s’échapper du plan pour se déplacer dans l’espace. Pour cela, on utilise
la primitive perspective. Bienvenue dans le monde de la perspective 3D !
Pour représenter l’espace en trois dimensions dans un plan à deux dimensions uniquement, on utilise une perspective
de projection. Une caméra observe la scène 3D et sa vision est projetée sur un plan intermédiaire. Voici un schéma
illustrant cette technique.
Certaines primitives vous permettent de positionner la caméra à votre guise, l’écran de projection étant situé à une
distance égale à la moitié de la distance caméra-origine du repère.
Dans le plan, la direction de la tortue était définie par son cap uniquement. Dans l’espace, l’orientation de la tortue
est donnée par 3 valeurs d’angles :
- Le roulis : Inclinaison de la tortue suivant l’axe (Oy)
- Le tangage : Inclinaison de la tortue suivant l’axe (Ox)
- Le cap : Inclinaison de la tortue suivant l’axe (Oz)
En fait, pour se déplacer dans l’espace la tortue, se comporte exactement comme un avion. Voici un petit schéma
permettant de se représenter ces trois grandeurs :
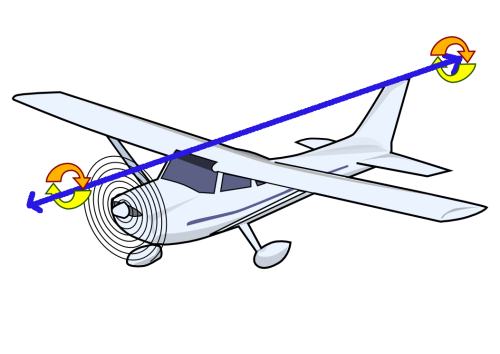 Le roulis
Le roulis
 Le tangage
Le tangage
 Le cap
Le cap
Cela peut paraitre compliqué de prime abord mais vous allez voir que beaucoup de choses se ramènent aux
déplacements usuels du plan. Voici les primitives élémentaires de déplacement dans l’espace :
Même comportement que dans le plan.
|
td, tournedroite, tg, tournegauche n |
| |
Meme comportement que dans le plan.
La tortue pivote sur la droite suivant son axe longitudinal de n degrés.
La tortue pivote sur la gauche suivant son axe longitudinal de n degrés.
La tortue pivote vers le haut suivant son axe transversal de n degrés.
La tortue pivote vers le bas suivant son axe transversal de n degrés.
Dans le plan pour tracer un carré de côté 200 :
repete 4[av 200 td 90]
Ces instructions restent valables dans l’espace, et le carré est tracé en perspective. Si l’on fait « piquer » la tortue
vers le bas de 90 degrés on peut tracer alors un nouveau carré.
ve
repete 4[av 200 td 90]
pique 90
repete 4[av 200 td 90]
Reste à s’entraîner pour appréhender toutes les orientations possibles !
Il faut toutefois bien comprendre que les trois primitives de rotation sont liées entre elles. Par exemple, testez la
séquence suivante :
ve
roulisgauche 90 cabre 90 roulisdroite 90
Le déplacement effectué revient à avoir
effectuer tournegauche 90 (Tester en
simulant la tortue avec votre main par
exemple...)
L’ensemble des primitives suivantes est valable dans l’espace comme dans le plan. La seule différence est la nature
des arguments attendus ou bien la nature des réponses. Par exemple, la primitive fpos ou fixeposition
attend toujours une liste comme argument, mais maintenant, il faut que cette liste contiennent trois
nombres (x;y;z) représentant les coordonnées spatiaux du point désiré. Voici un récapitulatif de ces
commandes :
Primitives compatibles dans le plan et dans l’espace
|
|
|
|
| cercle | arc | origine | vers |
|
|
|
|
| distance | fpos, fixeposition | fixex | fixey |
|
|
|
|
| fixecap | etiquette | longueuretiquette | point |
|
|
|
|
| pos, position | cap | | |
|
|
|
|
| |
Primitives valables uniquement en mode 3D
Cette primitive déplace la tortue au point de coordonnées indiqués. Elle attend donc trois arguments,
cette primitive est similaire à fpos mis à part que les coordonnées ne sont pas notés dans une liste.
Exemple, fixexyz -100 200 50 : déplace la tortue au point de coordonnées x = -100;y = 200;z = 50
Cette primitive déplace la tortue au point dont la cote z est égale à l’argument indiqué. Elle attend donc un nombre
comme argument, cette primitive est comparable à fixex ou fixey.
Positionne la tortue suivant l’inclinaison souhaitée. Cette primitive attend une liste contenant trois nombres,
respectivement le roulis, le tangage et le cap.
Exemple, fixeorientation [100 0 58] : la tortue prend pour roulis 100 degrés, pour tangage 0 degré et pour cap
58 degrés,.
Retourne l’orientation de la tortue sous forme d’une liste contenant respectivement le roulis, le tangage et le cap.
Attention à l’ordre de ces nombre, si par exemple, l’orientation est [100 20 90], ceci signifie que pour obtenir la
même orientation à partir de la position initiale (suite à avoir vider l’écran par exemple), il faudra
taper :
roulisdroite 100 cabre 20 tournedroite 90
Si vous permutez l’ordre de ces instructions, vous n’obtiendrez pas l’orientation désirée !
Fait pivoter la tortue suivant son axe longitudinal de telle sorte qu’elle adopte l’angle de roulis indiqué.
Retourne la valeur actuelle de l’angle de roulis.
Fait pivoter la tortue suivant son axe transversal de telle sorte qu’elle adopte l’angle de tangage indiqué.
Retourne la valeur actuelle de l’angle de tangage.
XLOGOest également muni d’un modeleur 3D qui vous permet d’afficher votre tracé en 3 dimensions. Ce module
utilise la bibliothèque JAVA3D qu’il est donc nécessaire d’installer si vous voulez profiter de cette
fonctionnalité.
Voici les consignes d’utilisation du modeleur :
Au fur et à mesure de vos tracés sur la zone de dessin, il faut indiquer au modeleur les formes géométriques qu’il
conservera pour un futur affichage. Il est possible d’enregistrer des polygones (surfaces), des lignes, des points ou
encore du texte. Pour cela, on dispose des primitives suivantes :
Tous les prochains déplacements seront enregistrés en vue de créer un polygone.
L’ensemble des sommets par lesquels est passé la tortue depuis l’appel de polydef matérialise un polygone dont la
couleur est déterminée par l’ensemble des sommets. Cette primitive finalise la création du polygone.
Tous les prochains déplacements seront enregistrés afin de créer une succession de segments.
L’ensemble des sommets par lesquels est passé la tortue depuis l’appel de lignedef matérialise une ligne brisée dont
l’écriture est ainsi finalisée.
Tous les prochains déplacements seront enregistrés afin de créer un ensemble de points.
L’ensemble des sommets par lesquels est passé la tortue depuis l’appel de pointdef sont enregistrés.
A chaque fois que l’utilisateur affichera un texte à l’aide de la primitive etiquette, celui-ci sera enregistré pour être
ensuite confier au modeleur 3D.
Fin de l’enregistrement des textes affiché à l’écran.
Lancement du modeleur 3D, tous les objets préalablement enregistrés sont affichés à l’écran.
Chaque face est un carré de 400 pas de tortue de côté. Voici le programme
pour carre
# Les sommets du carre sont enregistres
polydef repete 4[av 400 td 90] polyfin
fin
pour cubeSimple
# Cube jaune
ve perspective fcc jaune
# faces laterales
repete 4[carre lc td 90 av 400 tg 90 rd 90 bc]
# face du dessous
pique 90 carre cabre 90
# face du dessus
av 400 pique 90 carre
# Visualisation
vue3d
fin
On lance la commande cubeSimple :
Puis en remplaçant dans la procédure carre, polydef par lignedef et polyfin par lignefin
Si on utilisait pointdef et pointfin au lieu delignedef et lignefin, on aurait alors à l’écran uniquement les 8
sommets du cube. Ces deux primitives peuvent être tout particulièrement utilisées pour visualiser des nuages de
points dans l’espace.
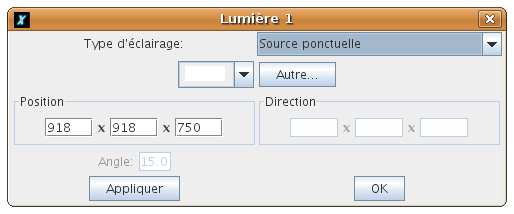
Vous avez la possibilité pour éclairer vos scènes 3D d’utiliser quatre lumières. Par défaut, la scène est éclairée par
deux lumières de type ponctuelle. Cliquer sur l’une des 4 ampoules dans le modeleur 3D, la boîte de dialogue
ci-dessous apparaît alors :
Plusieurs choix de lumières possible :
- Lumière ambiante : lumière uniforme, il est juste nécessaire de spécifier sa couleur
- Lumière unidirectionnelle : lumière éclairant suivant une direction constante. Cela correspond au cas
d’une source ponctuelle située très loin, par exemple, le cas du soleil.
- Lumière ponctuelle : lumière dont on connait la position, on pourrait comparer cette lumière à un
phare.
- Lumière de type « Spot » : c’est une lumière ponctuelle pour laquelle on peut restreindre l’éclairage au
sein d’un cône de lumière dont on doit spécifier l’angle.
Le meilleur est tout simplement de les essayer afin de comprendre leur fonctionnement respectif !
Vous avez la possibilité de rajouter un effet de brume sur votre scène 3D. Cliquer sur le bouton en forme de nuage
dans le modeleur 3D, la boîte de dialogue ci-dessous apparaît.
Deux types de brouillard au choix :
- Brouillard progressif : brouillard dont l’opacité devient de plus en plus importante. Vous devez spécifier deux
paramètres :
- La distance où le brouillard commence.
- La distance où l’opacité du brouillard est totale
- Brouillard uniforme : brouillard s’appliquant de manière uniforme à l’ensemble de la scène. Vous devez juste
spécifier ici le niveau de densité du brouillard.
Exemple avec un brouillard de type progressif :


 Le roulis
Le roulis Le tangage
Le tangage Le cap
Le cap