Interprétation par la tortue

14.2 Interprétation par la tortue

Ce premier exemple vous a permis d’appréhender la notion de système de Lindenmayer sans toutefois peut-être discerner comment nous allons utiliser cela concrètement avec la tortue.

C’est là que cela devient intéressant : Chacun des mots ainsi construits ne possède pas de signification particulière. On va alors attacher à chacune des lettres de la séquence, une commande à exécuter par la tortue et générer ainsi des dessins en 2D ou en 3D.

14.2.1 Symboles usuels

F : Se déplacer d’un pas unitaire (∈ V )
+ : Tourner à gauche d’angle α (∈ S).
− : Tourner à droite d’un angle α (∈ S).
& : Pivoter vers le bas d’un angle α (∈ S).
^ : Pivoter vers le haut d’un angle α (∈ S).
\ : Roulez vers la gauche d’un angle α (∈ S).
∕ : Roulez vers la droite d’un angle α (∈ S).
| : Effectuer un demi-tour. Avec XLogo : td 180

Prenons par exemple α = 90 et un déplacement unitaire de 10 pas de tortue, on obtient alors :

Symbole	F	+	−	&	^	\	∕	\|
Commande XLogo	`av 10`	`tg 90`	`td 90`	`pique 90`	`cabre 90`	`rg 90`	`rd 90`	`td 180`

14.2.2 Flocon de Koch

Considérons le L-system :

Etat initial : F −−F −−F −−
Règle de production : F → F + F −−F + F
Angle α = 60˚, le pas unitaire est divisé par 3 entre chaque itération.

Premières itérations :

Programme en Logo :

 
 pour flocon :p
 donne "unit 300/puissance 3 :p-1
 repete 3 [F :p-1 td 120]
 fin
 
 pour f :p
 si :p=0 [av :unit stop]
 F :p-1 tg 60 F :p-1 td 120 F :p-1 tg 60
 F :p-1
 fin

14.2.3 Courbe de Koch d’ordre 2

Intéressons-nous le L-system suivant :

Etat initial : F − F − F − F
Règle de production : F → F − F + F + FF − F − F + F

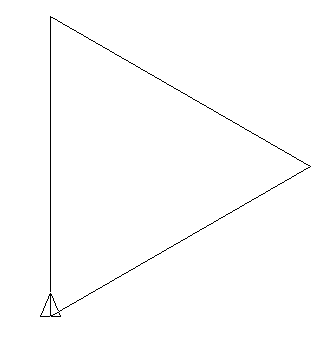
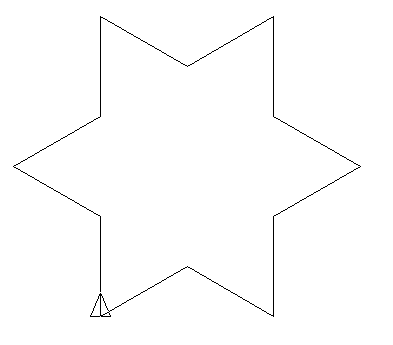
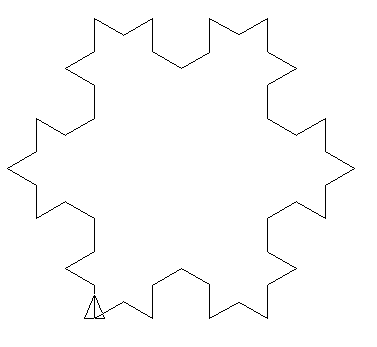
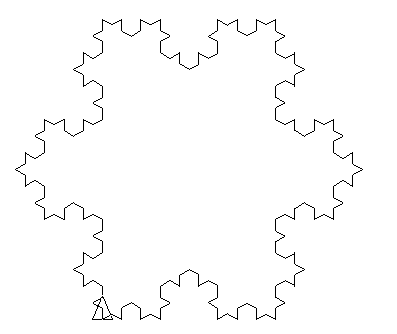
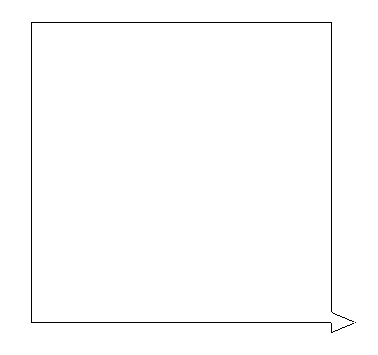
Voici les premières représentations en utilisant α = 90 et en ajustant le pas unitaire de telle sorte que la figure fasse toujours la même taille :

Il est alors très facile de créer le programme Logo permettant de générer ces dessins :

 # p désigne l’itération
 pour koch :p
 # Entre chaque itération, la distance unitaire est divisée par 4
 # Ici, la figure finale aura une taille de 600x600 au maximum
 donne "unit 300/puissance 4 :p-1
 
 repete 3 [F :p-1 tg 90] F :p-1
 fin
 
 # La chaine de réécriture
 pour F :p
 si :p=0 [av :unit stop]
 F :p-1 tg 90 F :p-1 td 90 F :p-1 td 90
 F :p-1 F :p-1 tg 90 F :p-1 tg 90 F :p-1 td 90 F :p-1
 fin

14.2.4 Courbe du dragon

Etat initial : F
Règle de production :

A → A + B+

B →−A − B

 pour a :p
 si :p=0 [av :unit stop]
 a :p-1 tg 90 b :p-1 tg 90
 fin
 
 pour b :p
 si :p=0 [av :unit stop]
                                                                                                  
                                                                                                  
 td 90 a :p-1 td 90 b :p-1
 
 fin
 
 pour dragon :p
 donne "unit 300/8/ :p
 a :p
 fin

dragon 10

dragon 15

14.2.5 Courbe de Hilbert en 3D

L’exemple suivant traite de la courbe de Hilbert dans l’espace, c’est une courbe qui a la propriété de remplir parfaitement un cube quand on augmente le nombre d’itérations.

Voici le L-system associé :

Etat initial : A
Angle α = 90˚, on divise la longueur unitaire par deux à chaque itération.

Règle de production :

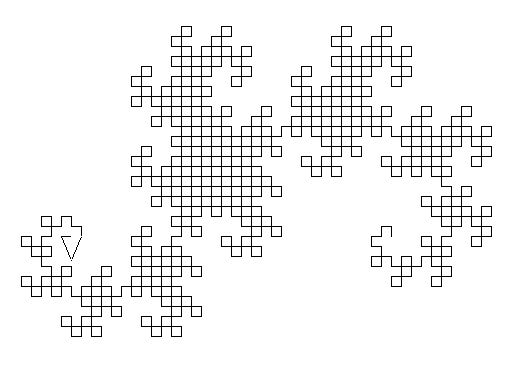
A → B − F + CFC + F − D&F^D − F + &&CFC + F + B∕∕

B → A&F^CFB^F^D^^ − F − D^|F^B|FC^F^A∕∕

C →|D^|F^B − F + C^F^A&&FA&F^C + F + B^F^D∕∕

D →|CFB − F + B|FA&F^A&&FB − F + B|FC∕∕

 pour hilbert :p
 ve perspective
 donne "unit 400/puissance 2 :p
 lignedef ftc :unit/2
 a :p
 lignefin
 vue3d
 fin
 
 pour a :p
 si :p=0 [stop]
 b :p-1 td 90 av :unit tg 90  c :p-1 av :unit c :p-1
                                                                                                  
                                                                                                  
 tg 90 av :unit td 90 d :p-1 pique 90 av :unit cabre 90 d :p-1
 td 90 av :unit tg 90 pique 180 c :p-1 av :unit c :p-1
 tg 90 av :unit tg 90 b :p-1 rd 180
 fin
 
 pour b :p
 si :p=0 [stop]
 a :p-1 pique 90 av :unit cabre 90 c :p-1 av :unit b :p-1 cabre 90
 av :unit cabre 90 d :p-1 cabre 180 td 90 av :unit td 90 d :p-1 cabre 90
 td 180 av :unit cabre 90 b :p-1 td 180 av :unit c :p-1 cabre 90 av :unit
 cabre 90 a :p-1 rd 180
 fin
 
 pour c :p
 si :p=0 [stop]
 td 180 d :p-1 cabre 90 td 180 av :unit cabre 90 b :p-1 td 90 av :unit tg 90
 c :p-1 cabre 90 av :unit cabre 90 a :p-1 pique 180 av :unit a :p-1 pique 90
 av :unit cabre 90 c :p-1 tg 90 av :unit tg 90 b :p-1 cabre 90 av :unit cabre 90
 d :p-1 rd 180
 fin
 
 pour d :p
 si :p=0 [stop]
 td 180 c :p-1 av :unit b :p-1 td 90 av :unit tg 90 b :p-1 td 180
 av :unit a :p-1 pique 90 av :unit cabre 90 a :p-1 pique 180 av :unit
 b :p-1 td 90 av :unit tg 90 b :p-1 td 180 av :unit c :p-1 rd 180
 fin

Et les premières itérations obtenues :