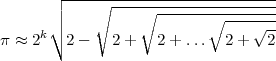
approximation We can approximate the number π using the formula:
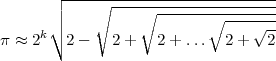
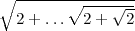 , so let’s code:
, so let’s code:
We found the first 5 digits! If we’re looking for more π digits, we have to allow a better precision with a higher number of digits while computing. Thus, we’re going to use the primitive setdigits.
And now, we have 39 digits...