Cubic Bezier Curve Base Class. More...

#include <_bezier.h>

Inheritance diagram for bezier_base< V, T >:

Public Types
typedef V	value_type
typedef T	time_type

Public Member Functions
	bezier_base ()
	bezier_base (const value_type &a, const value_type &b, const value_type &c, const value_type &d, const time_type &r=0.0, const time_type &s=1.0)
void	sync ()
value_type	operator() (time_type t) const
void	set_rs (time_type new_r, time_type new_s)
void	set_r (time_type new_r)
void	set_s (time_type new_s)
const time_type &	get_r () const
const time_type &	get_s () const
time_type	get_dt () const
bool	intersect_hull (const bezier_base< value_type, time_type > &) const
time_type	intersect (const bezier_base< value_type, time_type > &, time_type) const
	Bezier curve intersection function.
value_type &	operator[] (int i)
const value_type &	operator[] (int i) const

Protected Attributes
affine_combo< value_type, time_type >	affine_func

Private Attributes
value_type	a
value_type	b
value_type	c
value_type	d
time_type	r
time_type	s

Detailed Description

template<typename V, typename T = float>
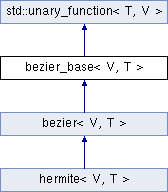
class bezier_base< V, T >

Cubic Bezier Curve Base Class.

Definition at line 71 of file _bezier.h.

Member Typedef Documentation

template<typename V, typename T = float>

typedef V bezier_base< V, T >::value_type

Definition at line 74 of file _bezier.h.

template<typename V, typename T = float>

typedef T bezier_base< V, T >::time_type

Definition at line 75 of file _bezier.h.

Constructor & Destructor Documentation

template<typename V, typename T = float>

bezier_base< V, T >::bezier_base ( )

inline

Definition at line 85 of file _bezier.h.

template<typename V, typename T = float>

bezier_base< V, T >::bezier_base	(	const value_type &	a,
		const value_type &	b,
		const value_type &	c,
		const value_type &	d,
		const time_type &	r = `0.0`,
		const time_type &	s = `1.0`
	)

inline

Definition at line 86 of file _bezier.h.

Member Function Documentation

template<typename V, typename T = float>

void bezier_base< V, T >::sync ( )

inline

Reimplemented in hermite< V, T >, and hermite< T >.

Definition at line 91 of file _bezier.h.

Referenced by bezier_base< T, float >::bezier_base(), bezier_base< float, float >::bezier_base(), bezier_base< double, float >::bezier_base(), and bezier< T, float >::subdivide().

template<typename V, typename T = float>

value_type bezier_base< V, T >::operator() ( time_type t ) const

inline

Definition at line 96 of file _bezier.h.

template<typename V, typename T = float>

void bezier_base< V, T >::set_rs	(	time_type	new_r,
		time_type	new_s
	)

inline

Definition at line 131 of file _bezier.h.

template<typename V, typename T = float>

void bezier_base< V, T >::set_r ( time_type new_r )

inline

Definition at line 132 of file _bezier.h.

Referenced by bezier< T, float >::subdivide().

template<typename V, typename T = float>

void bezier_base< V, T >::set_s ( time_type new_s )

inline

Definition at line 133 of file _bezier.h.

Referenced by bezier< T, float >::subdivide().

template<typename V, typename T = float>

const time_type& bezier_base< V, T >::get_r ( ) const

inline

Definition at line 134 of file _bezier.h.

Referenced by bezier< T, float >::evaluate(), bezier< T, float >::length(), and bezier< T, float >::subdivide().

template<typename V, typename T = float>

const time_type& bezier_base< V, T >::get_s ( ) const

inline

Definition at line 135 of file _bezier.h.

Referenced by bezier< T, float >::length(), and bezier< T, float >::subdivide().

template<typename V, typename T = float>

time_type bezier_base< V, T >::get_dt ( ) const

inline

Definition at line 136 of file _bezier.h.

Referenced by bezier< T, float >::evaluate(), and bezier< T, float >::subdivide().

template<typename V, typename T = float>

bool bezier_base< V, T >::intersect_hull ( const bezier_base< value_type, time_type > & ) const

inline

Definition at line 138 of file _bezier.h.

template<typename V, typename T = float>

time_type bezier_base< V, T >::intersect	(	const bezier_base< value_type, time_type > &	,
		time_type
	)		const

inline

Bezier curve intersection function.

Calculates the time of intersection for the calling curve.

I still have not figured out a good generic method of doing this for a bi-infinite cubic bezier curve calculated with the DeCasteljau algorithm.

One method, although it does not work for the entire bi-infinite curve, is to iteratively intersect the hulls. However, we would only detect intersections that occur between R and S.

It is entirely possible that a new construct similar to the affine combination function will be necessary for this to work properly.

For now, this function is BROKEN. (although it works for the floating-point specializations, using newton's method)

Definition at line 164 of file _bezier.h.

template<typename V, typename T = float>

value_type& bezier_base< V, T >::operator[] ( int i )

inline

Definition at line 215 of file _bezier.h.

Referenced by bezier< T, float >::find_closest(), and hermite< T >::sync().

template<typename V, typename T = float>

const value_type& bezier_base< V, T >::operator[] ( int i ) const

inline

Definition at line 219 of file _bezier.h.