14.1 Définition formelle

Un L-System est une grammaire formelle qui comprend :

1. Un alphabet V  : l’ensemble des variables du L-System. V ∗ est l’ensemble des "mots" que l’on peut construire avec les symboles de V , et V + l’ensemble des mots contenant au moins un symbole.
2. Un ensemble de valeur constantes S. Certains de ces symboles sont communs à tous les L-System. (Notamment quand on utilisera la tortue).
3. Un axiome de départ ω choisi parmi V + , c’est à dire l’état initial.
4. Un ensemble de règles, noté P, de reproduction des symboles de V .

Un L-System est alors noté {V,S,ω,P}.



Considérons le L-system suivant :

• Alphabet : V = {A,B}
• Constantes : S = {∅}
• Axiome de départ : ω = A
• Régles :

  A → AB

  B → A

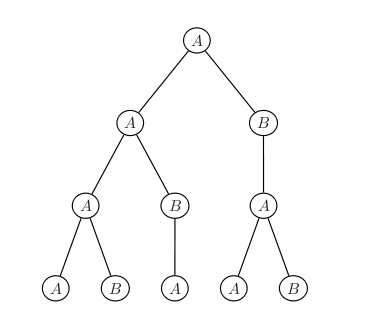
Les deux règles qui sont données sont les règles de réécriture du système. A chaque étape, A est remplacé par la séquence AB, et B est remplacé par A. Voici les premières itérations de ce système de Lindemayer :

• Itération 1 : A
• Itération 2 : AB
• Itération 3 : ABA
• Itération 4 : ABAAB

Bien, bien... et concrètement?? Lisons la suite!