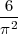 ≈ 0,6079. Pour essayer de retrouver ce résultat, voilà ce que l’on va faire :
≈ 0,6079. Pour essayer de retrouver ce résultat, voilà ce que l’on va faire :
En fait, un résultat connu de théorie des nombres établit que la probabilité que deux entiers pris au hasard
soient premiers entre eux est de 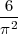 ≈ 0,6079. Pour essayer de retrouver ce résultat, voilà ce que l’on va faire :
≈ 0,6079. Pour essayer de retrouver ce résultat, voilà ce que l’on va faire :
pour test # On initialise la variable compteur à 0 donne "compteur 0 repete 1000 [ si (pgcd hasard 1000000 hasard 1000000)=1 [donne "compteur :compteur+1] ] ecris [frequence:] ecris :compteur/1000 fin |
Note : De même que précédemment, On est obligé de mettre des parenthèses sur pgcd hasard 1000000
hasard 1000000, sinon l’interpréteur va chercher à évaluer 1 000 000 = 1. Pour éviter ce problème de
parenthésage, écrire : si 1=pgcd hasard 1000000 hasard 1000000
On lance le programme test.
test 0.609 test 0.626 test 0.597 |
On obtient des valeurs proches de la valeur théorique de 0,6097. Ce qui est remarquable est que cette
fréquence est une valeur approchée de 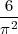 .
.
Si je note f la fréquence trouvée, on a donc : f ≈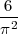
Donc π2 ≈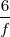 et donc π ≈
et donc π ≈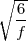 .
.
Je m’empresse de rajouter cette approximation dans mon programme, je transforme la fin de la procédure test :
pour test # On initialise la variable compteur à 0 donne "compteur 0 repete 1000 [ si 1=pgcd hasard 1000000 hasard 1000000 [donne "compteur :compteur+1] ] # On calcule la frequence donne "f :compteur/1000 # On affiche la valeur approchée de pi ecris phrase [approximation de pi:] racine (6/:f) fin test approximation de pi: 3.164916190172819 test approximation de pi: 3.1675613357997525 test approximation de pi: 3.1008683647302115 |
Bon, je modifie mon programme de tel sorte que quand je le lance, je précise le nombre d’essais souhaités. J’ai dans l’idée d’essayer avec 10000 essais, voilà ce que j’obtiens sur mes trois premières tentatives :
pour test :essais
# On initialise la variable compteur à 0
donne "compteur 0
repete :essais [
si 1=pgcd hasard 1000000 hasard 1000000 [donne "compteur :compteur+1]
]
# On calcule la frequence
donne "f :compteur/:essais
# On affiche la valeur approchée de pi
ecris phrase [approximation de pi:] racine (6/:f)
fin
test 10000
approximation de pi: 3.1300987144363774
test 10000
approximation de pi: 3.1517891481565017
test 10000
approximation de pi: 3.1416626832299914
|
Pas mal, non?