8.3 Un exemple de fractale : le flocon de Van Koch

Grâce à la récursivité, il est très facile de générer en LOGO des objets que l’on appelle en mathématiques des fractales.



Voici les premières étapes permettant de créer la ligne brisée de Van Koch.

Entre chaque étape :

1. chacun des segments est partagé en trois parties égales.
2. on trace un triangle équilatéral sur le deuxième segment.
3. on efface ce deuxième segment.

Ce qu’il faut remarquer : Prenons le cas de la deuxième étape, on constate que cette ligne est formée de quatre motifs correspondant à l’étape précédente et dont la taille est divisée par 3. On vient de mettre en évidence la nature récursive de la fractale.



Appelons L_n,ℓ le motif de longueur ℓ, tracé à l’étape n.

Pour tracer ce motif voici le procédé :

1. On trace L_{n−1,ℓ∕3}
2. On tourne à gauche de 60 degrés
3. On trace L_{n−1,ℓ∕3}
4. On tourne à droite de 120 degrés
5. On trace L_{n−1,ℓ∕3}
6. On tourne à gauche de 60 degrés
7. On trace L_{n−1,ℓ∕3}

En LOGO, cela donne tout simplement :

 # :l longueur du motif
 # :p étape
 pour ligne :l :p
 si :p=0 [av :l] [
   ligne :l/3 :p-1 tg 60 ligne :l/3 :p-1 td 120 ligne :l/3 :p-1 tg 60 ligne :l/3 :p-1
 ]
 fin
                                                                                                  
                                                                                                  

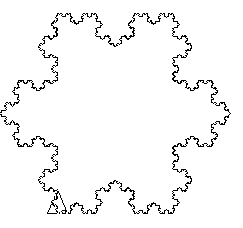
Si l’on trace un triangle équilatéral composé de trois de ces lignes, on obtient un magnifique flocon de Van Koch

 # :l longueur du côté
 pour flocon :l :p
 repete 3[ligne :l :p td 120]
 fin

Puis en lançant : flocon 200 6